| |
|
|
Онлайн-тестыТестыМатематика и статистикаМатематический анализвопросы331-345
331. Площадь параболического сегмента, ограниченного параболой 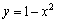 и осью и осью 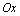 , равна: , равна:
• 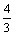
332. Площадь поверхности, образованной вращением вокруг оси 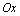 дуги дуги 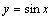 , , 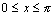 , вычисляется с помощью интеграла: , вычисляется с помощью интеграла:
• 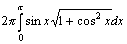
333. Площадь поверхности, образованной вращением вокруг оси 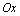 дуги кривой дуги кривой 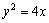 с концами в точках А (1, 2) и В (4, 4), вычисляется с помощью интеграла: с концами в точках А (1, 2) и В (4, 4), вычисляется с помощью интеграла:
• 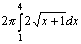
334. Площадь фигуры, ограниченной кривой r = a cos 2j, равна интегралу
• 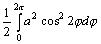
335. Полное приращение функции z = ¦ (x, y) в точке P0 (x0, y0) равно:
• ¦ (x0 + Dx, y0 + Dy) — ¦ (x0, y0)
336. Полным дифференциалом функции z = ¦ (x, y) в точке (x0, y0) называется:
• 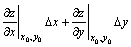
337. Полным дифференциалом функции z = ¦ (x, y) называется выражение
• 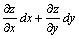
338. Последовательность , при 1/2 g 1/2 < 1 является:
• бесконечно малой
339. Последовательность 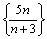
• ограниченная (1/2 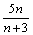 1/2 <= 5) 1/2 <= 5)
340. Последовательность 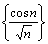 является: является:
• бесконечно малой
341. Последовательность может иметь
• только один предел
342. Потенциалом векторного поля 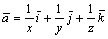 в области x > 0, y > 0, z > 0 является функция в области x > 0, y > 0, z > 0 является функция
• 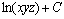
343. Производная 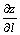 функции z = x3 — y2 в точке (1, 1) в направлении, задаваемом вектором функции z = x3 — y2 в точке (1, 1) в направлении, задаваемом вектором 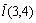 , равна: , равна:
• 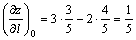 ( ( 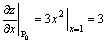 , , 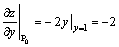 , , 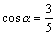 , , 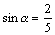 , a — угол наклона вектора , a — угол наклона вектора 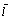 ) )
344. Производная  функции u = xyz в точке (1, 2, — 3) в направлении, задаваемом вектором функции u = xyz в точке (1, 2, — 3) в направлении, задаваемом вектором 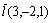 , равна: , равна:
• 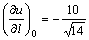 ( ( 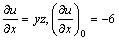 , , 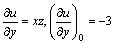 , , 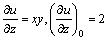 ; направляющие косинусы ; направляющие косинусы 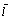 : : 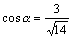 , , 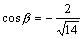 , , 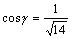 ) )
345. Производная функции ¦ (x, y) = 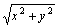 в точке (x0, y0) по направлению вектора в точке (x0, y0) по направлению вектора 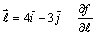 равна: равна:
• 
|
|
|

