| |
|
|
Онлайн-тестыТестыМатематика и статистикаМатематический анализвопросы466-480
466. У графика функции y = 3x3 — 2x2 + 6x — 1
• точка перегиба есть — это 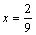
467. Уравнением касательной плоскости к поверхности 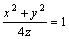 в точке (2, 2, 2) является: в точке (2, 2, 2) является:
• x + y — z — 2 = 0
468. Уравнением нормали к поверхности 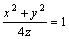 в точке (2, 2, 2) является: в точке (2, 2, 2) является:
• x — 2 = y — 2 = 2 — z
469. Функция 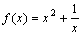 не является нечетной потому, что ... не является нечетной потому, что ...
• ¦ (- x) ¹ — ¦ (x), , например ¦ (1) = 2, ¦ (- 1) = 0
470. Функция 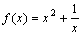 не является четной потому, что ... не является четной потому, что ...
• ¦ (-x) ¹ ¦ (x), например ¦ (1) = 2, ¦ (- 1) = 0
471. Функция 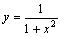 имеет интервалов монотонности — ... имеет интервалов монотонности — ...
• два
472. Функция  возрастает на: возрастает на:
• (-1, 1)
473. Функция 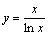 на интервале (0, ∞): на интервале (0, ∞):
• имеет минимум
474. Функция  на интервале (0, 4): на интервале (0, 4):
• монотонно возрастает
475. Функция ¦ (x, y) = y4 — 4y2  +y2+4x+4y имеет одну стационарную точку. Это точка ... +y2+4x+4y имеет одну стационарную точку. Это точка ...
• (4, -2)
476. Функция ¦ (x) называется нечетной, если ...
• ¦ (- x) = — ¦ (x) при всех x из области определения функции
477. Функция ¦ (x) называется четной, если ...
• ¦ (- x) = ¦ (x) при всех x из области определения функции
478. Функция y = x4 — 2x2 + 5 на интервале (-1, 1):
• имеет максимум
479. Функция y = x4 — 2x2 + 5 на интервале (-2, 0):
• имеет минимум
480. Функция y = x4 — 2x2 + 5 на интервале (0, -2]
• имеет минимум
|
|
|

